Min Distance to Furthest

INTERN

You are given a tree-shaped undirected graph consisting of n nodes labeled 1...n and n-1 edges. The i-th edge connects nodes edges[i][0] and edges[i][1] together.

For a node x in the tree, let d(x) be the distance (the number of edges) from x to its farthest node. Find the min value of d(x) for the given tree.

The tree has the following properties:

• It is connected.
• It has no cycles.
• For any pair of distinct nodes x and y in the tree, there's exactly 1 path connecting x and y.

Function Description
Complete the function findMinDistanceToFurthestNode in the editor. findMinDistanceToFurthestNode has the following parameters:

• int n : the number of nodes
• int edges[n-1][2] : an array of n-1 edges where each edges[i] contains two integers representing an edge connecting the nodes

Returns
int: the minimum distance to the furthest node

Example 1 : 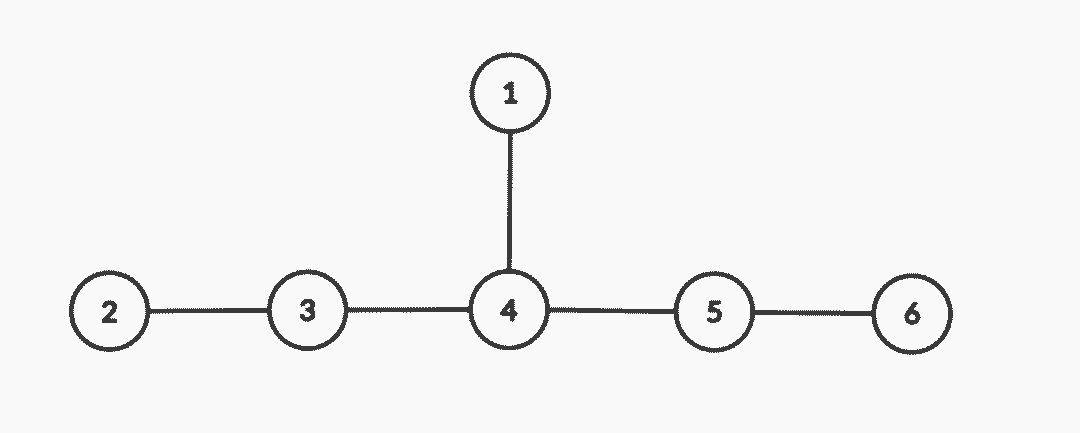Input:
n = 6, edges = [[1, 4], [2, 3], [3, 4], [4, 5], [5, 6]]
Output:
2

Example 2 : Input:
n = 6, edges = [[1, 3], [4, 5], [5, 6], [3, 2], [3, 4]]
Output:
2

Example 3 : 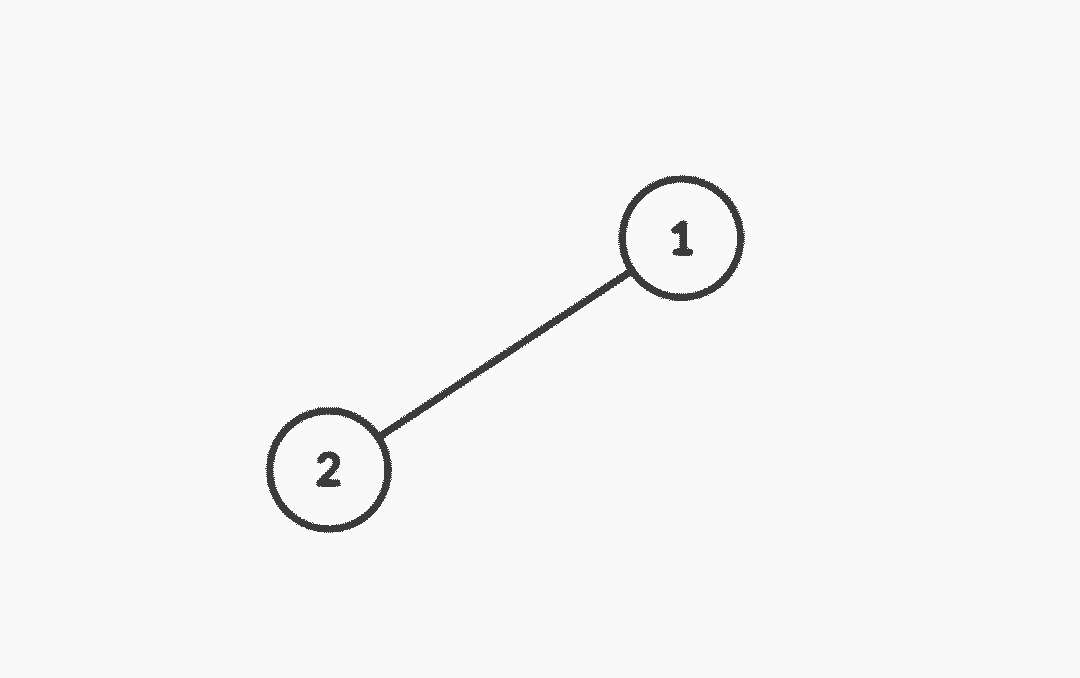Input:
n = 2, edges = [[1, 2]]
Output:
1

Example 4 : 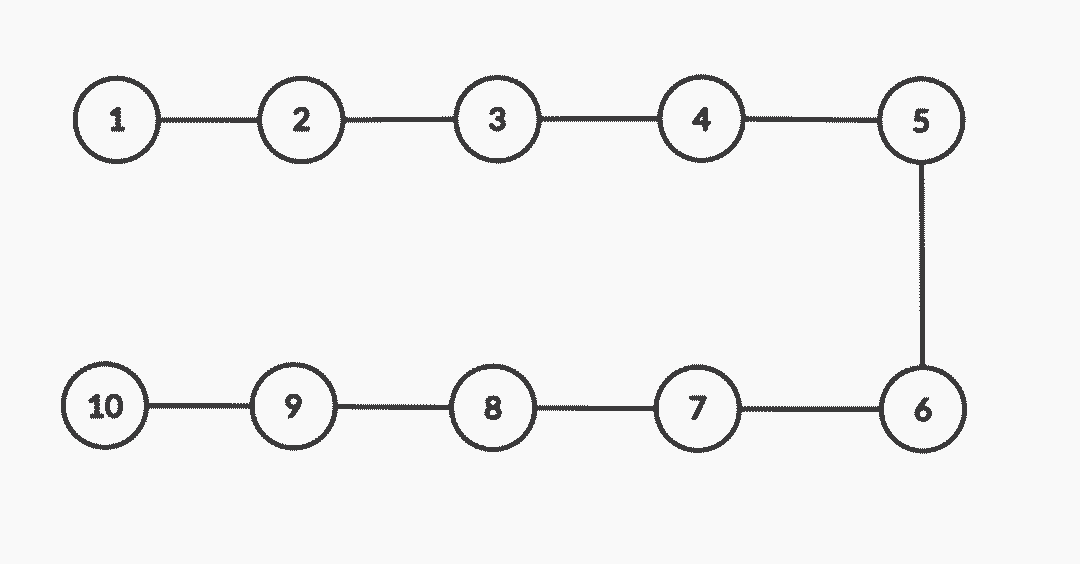Input:
n = 10, edges = [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], [7, 8], [8, 9], [9, 10]]
Output:
5

Example 5 :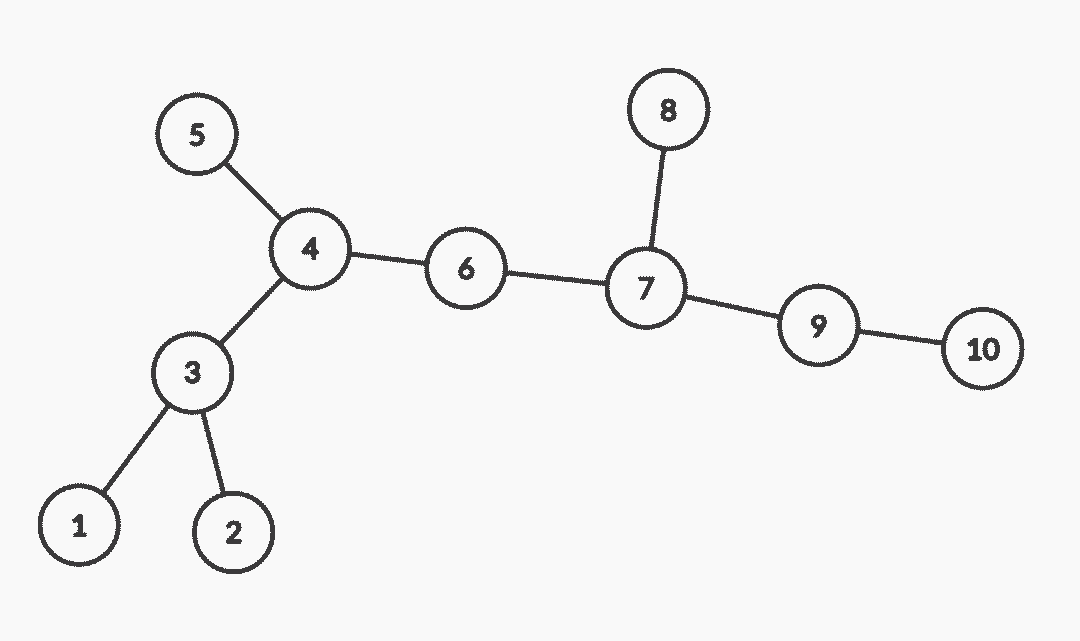

Input:
n = 10, edges = [[7, 8], [7, 9], [4, 5], [1, 3], [3, 4], [6, 7], [4, 6], [2, 3], [9, 10]]
Output:
3

Constraints:
You can assume that input is alwasy valid and satisfies all constraints.